Find the Solutions to X 2 18 Brainly

Graphing Quadratic Equations Using the Axis of Symmetry

A quadratic equation is a polynomial equation of degree $2$ .  The standard form of a quadratic equation is

$0=a{x}^2+bx+c$

where $a,b$ and $c$ are all real numbers and $a\ne 0$ .

If we replace $0$ with $y$ , then we get a quadratic function

$y=a{x}^2+bx+c$

whose graph will be a parabola .

The axis of symmetry of this parabola will be the line $x=-\frac{b}{2a}$ . The axis of symmetry passes through the vertex, and therefore the $x$ -coordinate of the vertex is $-\frac{b}{2a}$ . Substitute $x=-\frac{b}{2a}$ in the equation to find the $y$ -coordinate of the vertex. Substitute few more $x$ -values in the equation to get the corresponding $y$ -values and plot the points. Join them and extend the parabola.

Example 1:

Graph the parabola $y=x^2-7x+2$ .

Compare the equation with $y=a{x}^2+bx+c$ to find the values of $a$ , $b$ , and $c$ .

Here, $a=1,b=-7$ and $c=2$ .

Use the values of the coefficients to write the equation of axis of symmetry .

The graph of a quadratic equation in the form $y=a{x}^2+bx+c$ has as its axis of symmetry the line $x=-\frac{b}{2a}$ . So, the equation of the axis of symmetry of the given parabola is $x=\frac{-\left(-7\right)}{2\left(1\right)}$ or $x=\frac{7}{2}$ .

Substitute $x=\frac{7}{2}$ in the equation to find the $y$ -coordinate of the vertex.

$\begin{array}{l}y={\left(\frac{7}{2}\right)}^2-7\left(\frac{7}{2}\right)+2\\ =\frac{49}{4}-\frac{49}{2}+2\\ =\frac{49-98+8}{4}\\ =-\frac{41}{4}\end{array}$

Therefore, the coordinates of the vertex are $\left(\frac{7}{2},-\frac{41}{4}\right)$ .

Now, substitute a few more $x$ -values in the equation to get the corresponding $y$ -values.

$x$	$y=x^2-7x+2$
$0$	$2$
$1$	$-4$
$2$	$-8$
$3$	$-10$
$5$	$-8$
$7$	$2$

Plot the points and join them to get the parabola.

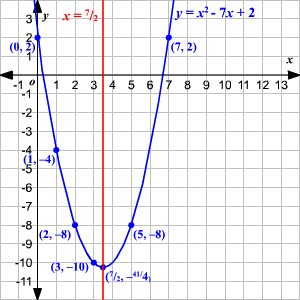
Example 2:

Graph the parabola $y=-2x^2+5x-1$ .

Compare the equation with $y=a{x}^2+bx+c$ to find the values of $a$ , $b$ , and $c$ .

Here, $a=-2,b=5$ and $c=-1$ .

Use the values of the coefficients to write the equation of axis of symmetry.

The graph of a quadratic equation in the form $y=a{x}^2+bx+c$ has as its axis of symmetry the line $x=-\frac{b}{2a}$ . So, the equation of the axis of symmetry of the given parabola is $x=\frac{-\left(5\right)}{2(-2)}$ or $x=\frac{5}{4}$ .

Substitute $x=\frac{5}{4}$ in the equation to find the $y$ -coordinate of the vertex.

$\begin{array}{l}y=-2{\left(\frac{5}{4}\right)}^2+5\left(\frac{5}{4}\right)-1\\ =\frac{-50}{16}+\frac{25}{4}-1\\ =\frac{-50+100-16}{16}\\ =\frac{34}{16}\\ =\frac{17}{8}\end{array}$

Therefore, the coordinates of the vertex are $\left(\frac{5}{4},\frac{17}{8}\right)$ .

Now, substitute a few more $x$ -values in the equation to get the corresponding $y$ -values.

$x$	$y=-2x^2+5x-1$
$-1$	$-8$
$0$	$-1$
$1$	$2$
$2$	$1$
$3$	$-4$

Plot the points and join them to get the parabola.

Example 3:

Graph the parabola $x=y^2+4y+2$ .

Here, $x$ is a function of $y$ . The parabola opens "sideways" and the axis of symmetry of the parabola is horizontal. The standard form of equation of a horizontal parabola is $x=a{y}^2+by+c$ where $a$ , $b$ , and $c$ are all real numbers and $a\ne 0$ and the equation of the axis of symmetry is $y=\frac{-b}{2a}$ .

Compare the equation with $x=a{y}^2+by+c$ to find the values of $a$ , $b$ , and $c$ .

Here, $a=1,b=4$ and $c=2$ .

Use the values of the coefficients to write the equation of axis of symmetry.

The graph of a quadratic equation in the form $x=a{y}^2+by+c$ has as its axis of symmetry the line $y=-\frac{b}{2a}$ . So, the equation of the axis of symmetry of the given parabola is $y=\frac{-4}{2\left(1\right)}$ or $y=-2$ .

Substitute $y=-2$ in the equation to find the $x$ -coordinate of the vertex.

$\begin{array}{l}x={\left(-2\right)}^2+4\left(-2\right)+2\\ =4-8+2\\ =-2\end{array}$

Therefore, the coordinates of the vertex are $\left(-2,-2\right)$ .

Now, substitute a few more $y$ -values in the equation to get the corresponding $x$ -values.

$y$	$x=y^2+4y+2$
$-5$	$7$
$-4$	$2$
$-3$	$-1$
$-1$	$-1$
$0$	$2$
$1$	$7$

Plot the points and join them to get the parabola.

Find the Solutions to X 2 18 Brainly

Source: https://www.varsitytutors.com/hotmath/hotmath_help/topics/graphing-quadratic-equations-using-the-axis-of-symmetry

Share :